At present, AGF (artificial ground freezing) technique is a mature construction method, which has been widely used in such fields as mine engineering, tunneling engineering, temporary foundation, reinforcement, ground water pollution control, waste landfills. During construction, significant engineering parameters such as the width and mechanical properties of frozen soil wall, are determined by the temperature field of frozen soil wall, thus making the theory of temperature field the basis for AGF theory.

Among the main calculating methods of temperature field of ground freezing (analytical method, simulation and numerical analysis), analytical method is always a key part in the study of temperature field because of its theoretical advantages. 

So far, a series of classical analytical solutions of steady-state temperature field have been made. But the solving method to steady-state temperature field of artificial ground freezing has not been summarized systematically and there is no explicit solving method to direct the subsequent freezing problem.

The Analytical Solving Method to Steady-State Temperature Field of Artificial Ground Freezing should be studied and obtained.

 

Objective:

Obtains the Solving Method to Steady-State Temperature Field of Artificial Ground Freezing and gives solutions to some freezing problems that the arrangement of freezing pipe is in common such as multi-pipe freezing, row-pipe freezing and circle-pipe freezing.

 

Approach:

Based on the theory of analogy between thermal and hydraulic problems, the means of superposition of potential is introduced in artificial ground freezing and it is the based approach to solve freezing problems. Then conformal mapping and mirror reflection method is introduced to direct complex freezing problems.

Based on the separability of boundary conditions for Laplace equations, the means of decomposition of function as an expended approach is introduced in artificial ground freezing

 

Significant Results and Potential Impact:

Means of superposition of potential: many classic solutions are derived again and many spilt-new solutions are obtained such as few-pipe freezing solution, three-row-pipe freezing solution. This means offers the possibility to solve the pending problem.

Means of decomposition of function: the circle-pipe freezing solution is given perfectly. As an expended approach, this means makes the more freezing problems solved.

 

Principal Investigator:

Xiangdong HU 

 

Multi-pipe freezing:

  

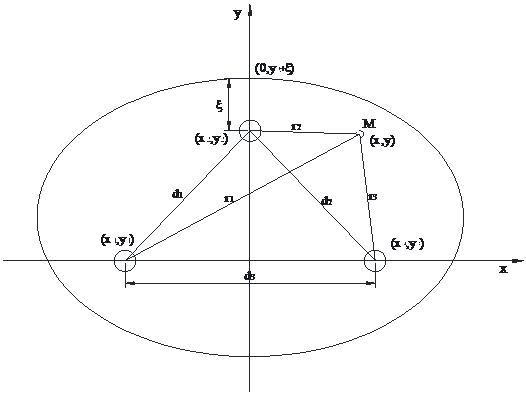
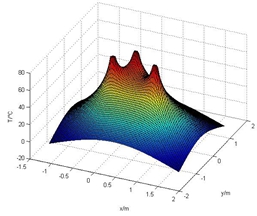
Three freezing pipes arranged at random in the infinite region

 

  

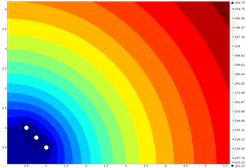
Three freezing pipes arranged near a right angle adiabatic boundary

 

Multi-row-pipe freezing:

   

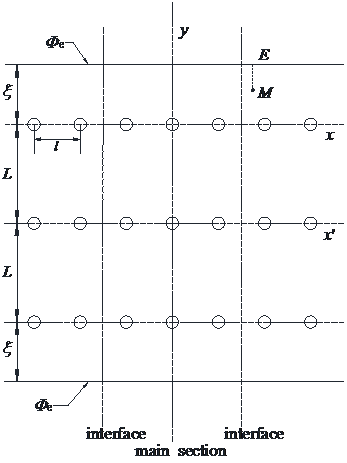
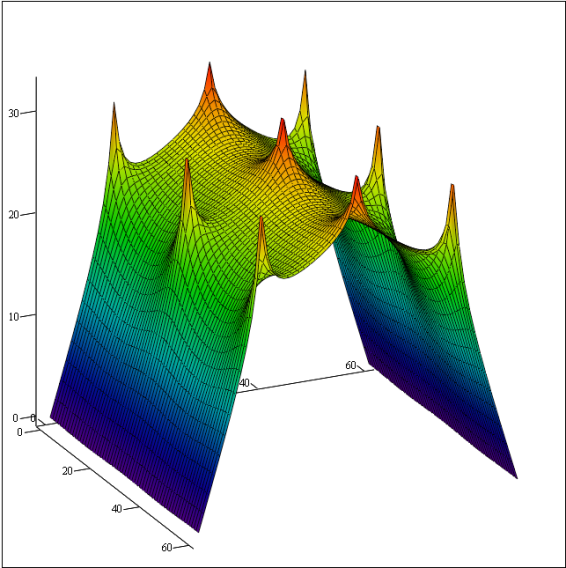
The aligned three-row freezing pipes and their constant potential boundaries

 

 

Multi-circle-pipe freezing:

 

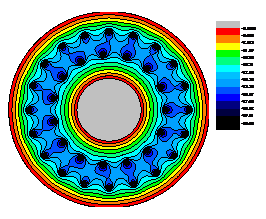
Model of single- and double-circle-pipe freezing